Developments12 分钟 读完 (大约 1804 个字)

[Leetcode] Q5最长回文串

边界问题

Q5: Longest Palindromic Substring

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

1
2
3
Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.

Example 2:

1
2
Input: "cbbd"
Output: "bb"

最暴力的手段当然就是把所有的子串全部列出来，并逐个判断是否符合“palindrome”回文数的标准，光是想一想就觉得很麻烦。

此时有一个更符合直觉的想法：将字符串倒过来，这样就将“寻找最大回文串”转变成了“寻找公共子串”的问题，当然二者还是有一些小小的区别的，且看后文。

  

解法1：倒序+最大公共子串

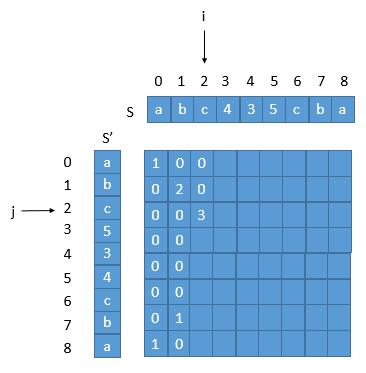
此时不妨以babad为例，以字符串origin_str和倒序字符串reverse_str构建一个二维数组(脑力不够，纸笔来凑)：

每当出现字符相等的情况：array[i][j] = array[i-1][j-1] + 1

字符不想等的情况：array[i][j] = 0

此时数组中记录的最大数值，即为最长的公共子串的长度。

Reverse

当然还有几个细节需要考虑：

  • 存在maxLen = arr[i][j]显示出长度，同时[i][j]也可以指明“坐标”，通过偏移量直接用切片获取目标字符串；

边界情况：

  • i==0或j==0的情况下，直接将符合字符相等情况的位置标记 1
  • 字符出和逆序字符串可能存在“错位相等”的情况，以标记最大长度的点，判断“倒序后的坐标”和“原坐标”是否相符

  

代码部分：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func longestPalindrome(s string) string {
	reverse := leetutils.Reverse(s)
	maxLen := 0
	index := 0
	l := len(s)
	mtx := make([][]int, l)
	for i := 0; i < l; i++ {
    // 初始化，默认值都为0
		mtx[i] = make([]int, l)
		for j := 0; j < l; j++ {
      // 字符相同
			if s[i] == reverse[j] {
        // 边界处理
				if i == 0 || j == 0 {
					mtx[i][j] = 1
				} else {
					mtx[i][j] = mtx[i-1][j-1] + 1
				}
			}
      
      // 更新maxLen
			if mtx[i][j] > maxLen {
        // 判断末尾元素在s和reverse中是否是同一个元素
				if (l - 1 - j + mtx[i][j] - 1) == i {
					maxLen = mtx[i][j]
					index = i - maxLen + 1
				}
			}
		}
	}
	return s[index : index+maxLen]
}

最后更新maxLen的判断，也可以使用另外一种方法：对比“目标子串”是否回文（感觉会引来更多的边界）

这种思路总的来说还是比较自然且简单的，主要的麻烦集中在几个边界问题的处理上。当然因为思路比较简单，导致不管是时间复杂度O(n^2) 还是空间复杂度O(n^2)都是比较高的。

解法2：中心扩展

中心扩展其实也很好理解，回文串肯定是对称的，在一次遍历中，对字符向两边进行扩展，碰到左右相同时就继续，不同时退出。

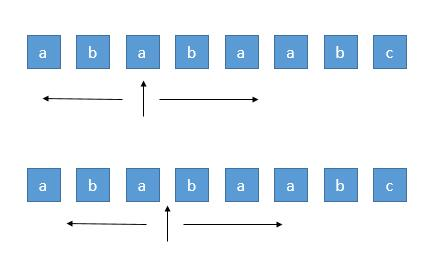
Center Spread

边界问题：

  • 回文串的长度“奇数/偶数”需要分别考虑
  • 扩展“碰壁”时的处理

  

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
func longestPalindrome(s string) string {
	i := 0
	l := ""
	temp := ""
	for i < len(s) {
		// 奇数
		temp = getPalindrome(s, i, i)
		if len(l) < len(temp) {
			l = temp
		}
		// 判断是否会越界
		if i+1 < len(s) {
			// 偶数
			temp = getPalindrome(s, i, i+1)
			if len(l) < len(temp) {
				l = temp
			}
		}
		i++
	}
	return l
}

// getPalindrome 向两边延伸找到最大回文串
func getPalindrome(s string, left int, right int) string {
	for left >= 0 && right < len(s) {
		if s[left] == s[right] {
			left--
			right++
		} else {
			// 左右不相同，回退
			left++
			right--
			break
		}
	}
	// 碰到字符串边界的处理
	if left < 0 || right >= len(s) {
		return s[left+1 : right]
	}
	return s[left : right+1]
}

结合上面的图片和代码中的注释，还是很好理解的，在字符串问题解题过程中经常遇到的就是“越界”，因此在写代码的时候要时刻注意判断。

中心扩展法的时间复杂度是O(n^2)，空间复杂度是O(1)，就提交的情况来看，性能会远高于第一个算法。

  

解法3：Manacher’s Algorithm

Manacher算法理论上可以将算法的时间复杂度降到O(n)，事实上就是在“中心扩展”算法基础上进一步优化，减少了计算“回文串”的次数。

预处理：插入#

为了解决奇数偶数处理逻辑不一样的问题，这里有个巧妙的方法：在每个字符间插入#，并在开头结尾分别插入^# #$，这时你会发现字符串的长度一定是一个奇数。这样在进行中心扩展的时候，处理的永远是奇数长度的字符串了。

Insert #

求P[i]

对每个位置为i的点，以其为对称中心，左右对称点的个数即为P[i]（包括#，后文我们称P[i]为回文半径），如下图：

p[i]

上图中的C(center)，便是计算的中心，如果将C从头到尾遍历一次，那就是“中心扩展”算法了，Manacher的核心就是跳过不必要的C，以此提高计算的效率。

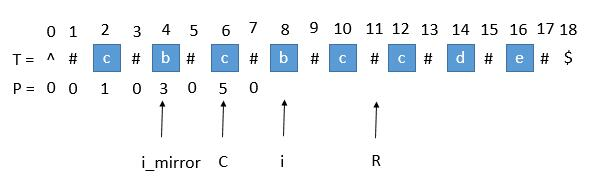
travel

以上图为例，C为对称中心，对称半径为5，那么可以判定处于T[6-5 : 6+5]即T[1 : 11]内的所有对称点(i与i_mirror)都具有相同的属性.

i从C的临近出逐渐远离，P[i]的作用是预先确定回文半径，因此我们至少可以判定i所指的P[i]至少为3，当i处开始中心扩展时，就可以从3开始，节省了时间。

​

依然很重要的边界问题 :

  • P[i]受到P[i_mirror]与边界R的限制，为其中的较小值，原因是当i+P[i_mirror]可能会超出边界R，超出边界时，就需要更新中心C与边界R；
  • 在i向右侧展开时，依然要对每个点进行“中心展开”，但由于P[i_mirror]可以一定程度避免重复计算；

​

提取目标回文串

可以发现i减去P [ i ]，再除以 2，就是原字符串的开头下标了，所以利用最大的P[i]与其位置i，就可以从原字符串中提取出目标回文串。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
func longestPalindrome3(s string) string {
	origin := s
	s = pretreatment(s)
	len := len(s)

	// p[] 存储各个点上的中心扩展(回文)值
	p := make([]int, len)
	var center, bound, maxLen, centerIndex int

	p[0] = 0
	p[1] = 0
	center = 1

	// 对right点 确定p[right]
	for right := 1; right < len-1; right++ {
		left := 2*center - right

		// 超出边界
		if right > bound {
			p[right] = 0
		} else {
			// 取left，bound-i (到边界的距离)，p[left] (镜像位置)
			p[right] = int(math.Min(float64(bound-right), float64(p[left])))
		}

		// 对正在处理的right点，尝试中心扩展
		for s[right+1+p[right]] == s[right-1-p[right]] {
			p[right]++
		}

		// 超出界限, 更新 center 和 bound
		if (right + p[right]) > bound {
			center = right
			bound = right + p[right]
		}
	}

	for i := 1; i < len-1; i++ {
		if p[i] > maxLen {
			maxLen = p[i]
			centerIndex = i
		}
	}
	startIndex := (centerIndex - maxLen) / 2
	return origin[startIndex : startIndex+maxLen]

}

func pretreatment(s string) string {
	len := len(s)
	if len == 0 {
		return "^$"
	}
	cue := []rune("^#$")
	var res []rune
	runes := []rune(s)
	res = append(res, cue[0])
	for i := 0; i < len; i++ {
		res = append(res, cue[1], runes[i])
	}
	res = append(res, cue[1], cue[2])
	return string(res)
}
#

最新文章

×